Mechanism for the Absorption of Light
The formalism for the absorption of light in the simplest case starts with a beam of light of intensity I of photons that has just penetrated into a material with a uniform concentration of absorbing pigments. We ignore reflection and refraction. The photons penetrate into the material and are absorbed at different depths (Fig. 1).
Figure 1. Schematic of light rays penetrating to different depths into a photon absorbing material
The mechanism for absorption is that a photon transfers all its energy to an electron in the absorbing material. The photon is "lost" from the light beam as it is absorbed in a single event. The electron is excited by the gain in energy to a higher energy state in the electron configuration around the atom. This single-event transfer of photon energy to an electron and the disappearance of the photon is closely related to the photoelectric effect where the electron is ejected from the material in a single event. The electron is ejected from the atom by the absorption of an x-ray. This loss of an electron leaves the atom in an excited state.
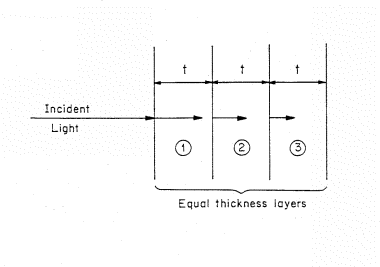
Figure 2. Light incident on a light absorbing material that is represented by a stack of equivalent thickness, t, layers. The length of the arrows decrease as the light penetrate showing the decreasing intensity of light.
The decrease in intensity of the light or photon flux as the beam penetrates into the material can be visualized if we separate the absorbing material into a set of thin, equal thickness slices of thickness t (Fig. 2). The material is homogeneous and the thickness t is chosen so that only a small fraction of the light is absorbed in passing through the layer. The symbol A is used to denote the fraction absorbed. The fraction of light absorbed in the first layer is (1-A) times the incident intensity. For example, if the fraction of light absorbed per layer is 10% of the incident flux, then for 100 photons incident on the first layer, AI=0.1 x 100 or 10 will be absorbed and 90 transmitted to the second layer.
The light intensity incident on the second layer is (1-A)I and A(1-A)I will be absorbed on the second layer. The amount transmitted through the second layer is (1-A)2I. To continue our example, with 90 photons incident on the second layer, A x 90 = 0.1 x 90 = 9 photons will be absorbed and 81 transmitted. That is:
-
Layer 1, I photons incident, AI=0.1x100 = 10 absorbed and
-
(1-A)I=(1-.1)100=90 transmitted
-
(1-A)(1-A)I=(0.9)(0.9)100=81 are transmitted.
The process continues with fewer photons being transmitted into layer 3, layer 4, and so on, with fewer photons being absorbed in each successive layer although the fraction absorbed A remains constant.
The absorption of photons is given in more general form in Table 1 for an absorbed fraction A.
| Table 1. Transmission for absorbed fraction A | |||
| Incident on layer | Absorbed in layer | Transmitted through layer | |
| layer 1 | I | AI | (1-A)I |
| layer 2 | (1-A)I | A(1-A)I | (1-A)2I |
| layer 3 | (1-A)2I | A(1-A)2I | (1-A)3I |
| layer n | (1-A)n-1I | A(1-A)n-1I | (1-A)nI |
For n layers, the total absorption TA in all layers absorbed
fraction A will be
The total transmitted light TT though n layer is
Equation 1 is more conveniently written using an exponential function.
Using an absorption coefficient alpha, the intensity of light at depth
t, I(t) for an incident intensity I0 is given by
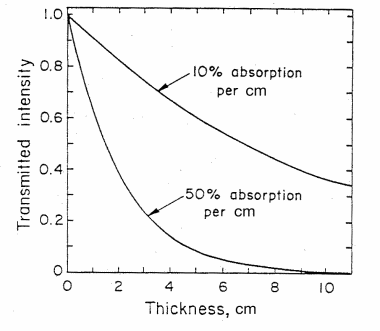
Figure 3. The intensity of light transmitted through an absorbing material as a function of thickness d in cm for (1) 10% absorbance and (2) 50% absorbance per cm. (from T. B. Brill, Light (Plenum Press, New York, 1980))
The relations rely on the fact that the fraction of light which is absorbed
is independent of the intensity of the incident light. For a given wavelength
of light, each successive equi-thickness of the medium aborbs an equal
fraction of light passing through it, but the amount of light it receives
is sucessively decreasing. Hence, the intensity of light passing though
a medium will decrease with depth. The exponential attenuation coefficients
apply for x-rays as well as photons in the visible portion of the electromagnetic
spectrum. The exponential relation is derived in the following:
The number of deltaI of photons which are absorbed in a given thickness
deltax is proportional to the incident intensity I or the number I incident
on it:
The absorption coefficient is a number per unit distance, such as 0.1 per cm which can be written 0.1 cm-1. At a depth x where alpha x equals unity (in this example, x=10 cm as 0.1 x 10 =1) the number of photons decreases by a factor of 1/e or 0.37 (the value of e=2.718).
For small values of alpha x, for example alpha x =0.01, Eqn 7 can be written as a linear expansion:
For x-rays, photoelectric absorption (where the x-ray gives up its energy in a single interaction with an electron) is the major cause of attenuation of the photons penetrating the material.
The intensity I of x-rays transmitted through a thin foil of material for an incident intensity I0 follows the exponential attenuation relation of equation 3 with a change in the nomenclature from alpha to mu to follow the convention of in standard x-ray usage:
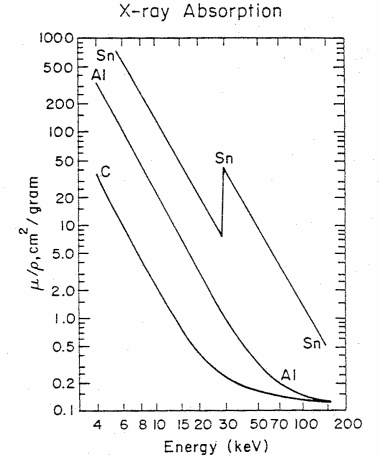
Figure 4. The x-ray mass absorption coefficient (mu/rho) in cm2/gram versus x-ray energy in kiloelectron volts (keV) for carbon (C), aluminum (Al), and tin (Sn). The sharp increase in absorption for Sn at 29.2 keV corresponds in energy to the K-shell, 1s binding energy (taken from Feldman and Mayer, Fundamentals of Surface and Thin Film Analysis, (North Halland, New York. 1986))
Table 2 gives the density and mass absorption coefficient at two wavelengths of several elements found in artists pigments. One notes from the table, that the mass absorption coefficient tends to increase with increase in atomic number (Z) and that the absorption coeficient is greater (in some cases a factor of ten greater) for the longer wavelength (lower energy) photons. There are apparent anomalies with the absorption of Cd at 0.711Å less than that of arsenic. This is due to the electronic structure and binding energies of electrons. Figure 4 gives the mass attenuation coefficient as a function of energy for several elements. This shows both the strong energy dependence of the absorption coefficient (mu/rho decreases with increasing energy) and the five to ten fold jumps in absorption at specific energies. These jumps occur when the energy of the photon exceeds the binding energy of the electrons.
| Table 2. Atomic Number (Z) Element density, rho in gm/cm3 and mass attenuation coefficient in cm2/gm at wavelengths of 0.711 and 1.54 Å | ||||
| Z | Element | Density
(gm/cm3) |
Mass Attenuation
Coeff. (cm2/gm)
|
|
| 17.4keV
0.711 Å |
8.05 keV
1.542 Å |
|||
| 22 | Titanium | 4.51 | 23.25 | 202.4 |
| 26 | Iron | 7.87 | 37.4 | 304.4 |
| 29 | Copper | 8.93 | 49.3 | 51.5 |
| 33 | Arsenic | 5.78 | 65.9 | 75.6 |
| 48 | Cadmium | 8.65 | 27.3 | 229.3 |
| 80 | Mercury | 13.55 | 114.7 | 216.2 |
| 82 | Lead | 11.34 | 122.8 | 232.1 |
